Mixtures of Experts
How to scale up models without increasing compute
When deploying machine learning models, inference costs hurt more than training costs. A model need only be trained once - and can be based on a predecessor - but the cost of running GPUs in production can be prohibitive. Unfortunately, the best neural networks have high parameter counts - and their performance increases with scale. Consequently, sparse models - where, for a particular input, only the most relevant parameters are used - have become popular. These enable the total parameter count to be increased, while holding constant the number of floating point operations required at inference.
A mixture of experts is a technique in which observations are routed to the parts of the model - the ‘experts’ - best positioned to deal with them. If not all experts are used, the model is sparse. Mixtures of experts train faster than dense models, are more accurate and require less compute at inference time. However, due to their high parameter count, more complex architecture and the need to distribute them across multiple GPUs, careful attention must be paid to routing, load balancing, training instabilities and the inference-time provisioning of experts across devices.
Architecture
In principle, each expert can have its own architecture. Mostly, this is not done - compared to other optimisations, the benefits are limited. While it might help to use different architectures for different modalities, within each modality the default choices (Transformers for text, CNNs or Vision Transformers for images) tend to be sufficiently powerful. Moreover, there are practical reasons not to:
At inference time, an expert might not be available - e.g. if it is oversubscribed. In this case, it helps if experts are not too divergent, so that the data can be routed to the next best expert.
Using a slower expert will hold up the rest of the batch and harm GPU utilisation.
Transformers
In a Transformer, a mixture of experts is normally implemented by replacing the feedforward network in each block (or in every other block) with N distinct feedforward networks and a lightweight router that sends data to at most k of them, as shown in Figure 1.1 Under this setup, each Transformer block has its own conditional computation step, and hence the expert networks are distributed throughout the stack. In each block, the attention heads first mix data between timesteps. Then, at each timestep, the k best experts are selected by the router; these operate on the timestep’s hidden state independently. The outputs from each of the activated experts - and the residual bypass connection - are then combined and proceed to the next part of the model.
If the data are multimodal, it might be worthwhile to also compute the attention heads conditionally. However, if the relationship between tokens are not so domain-dependent that they need to be computed separately, then this specialisation would be wasteful. A Transformer block typically contains multiple attention heads - or, at least, multiple query matrices - so different relationships can be learned. Though mixtures of experts do not require more computation, each specialised expert requires more memory - and GPU memory is expensive. The attention heads account for a high proportion of a Transformer’s parameters.2 Consequently, if there are fewer benefits to specialising them, it makes sense not to.
Nonetheless, Transformers in which the attention heads are separated into experts do exist. One notable example is the Branch-Train-Merge large language model, in which no parameters - except for the router - are shared. While this reduces or, if each expert is small enough, eliminates the costly communication overhead between GPUs at training and inference time, it is only viable in production if the demand for each expert can be accurately forecast. Otherwise, some models - and GPUs - will sit idle and others will be overloaded.
Routing
Token routing
Determining the best expert to process a token is a discrete optimisation problem. Discrete optimisation problems are not differentiable and hence, to learn the optimal allocation of tokens using backpropagation, a ‘soft’ assignment needs to be made instead.3 This is done by weighting the output of the experts E1, E2, …, EN by the trainable function R. Let x be the token vector and y be the summed output of the expert layer. Then, not forgetting to include a residual connection,
The router function R is parametrised in terms of a trainable weight matrix W, whose input dimension is equal to the dimension of the token vector x and whose output dimension is equal to the number of experts N.4 A naïve implementation of R is as a softmax:
However, in this form, each expert has a strictly positive weight R(x)i. This means that the mixture of experts is not sparse: every expert output Ei(x) must be computed. Instead, R is modified so that the k highest values of R(x) are retained and the rest are set to 0:
Originally, it was thought to be necessary to route to k ≥ 2 experts, as the model could not possibly learn how to route tokens if it could not directly compare experts. However, this is not so: k = 1 also works well. The reason for this is the residual connection. If an expert hurts performance, its parameters are modified - so that next time, it hopefully performs better - and it is downweighted. If, for a particular subset of tokens, the expert continues to do badly, it will fall out of the top k and the next best expert will be chosen instead.
Load balancing
If too many tokens are allocated to a particular expert, the expert will be oversubscribed and unable to process them all. When this happens, tokens can either be assigned to the next best expert or they can be ‘dropped’ - i.e. expert computation is omitted and the token representation propagates to the next layer through the residual connection. Even if expert capacity is overprovisioned or fully elastic, it is important to prevent a ‘winners get bigger’ effect: a positive feedback loop in which one expert becomes better and better at handling all tokens compared to the other untrained experts, so that the mixture of experts model becomes functionally equivalent to a dense model with redundant parameters.
To encourage a roughly equal allocation of tokens across experts, a load balancing term is added to the model’s training loss. This is done by penalising high router weights. Let B be a batch consisting of T tokens, N be the number of experts, f(i) be the fraction of tokens in the batch dispatched to expert i, p(i) be the fraction of the router weights assigned to expert i over the entire batch, R be the router weights outlined above. Fedus et al (2021) propose adding the following loss term for every expert layer:
where α is hyperparameter that reflects the importance assigned to load balancing. The the fraction of tokens in the batch dispatched to expert i is
and the fraction of the router weights assigned to expert i over the batch is
So the loss term is, essentially, the sum of the k highest router weights for each token in the batch5, multiplied by the scaling factors N, k and T and the hyperparameter α. (These scaling factors are there to ensure that the loss is invariant to changes in the total number of experts, the number of experts chosen for each token and the batch size.) The loss term is minimised when R(x)i = 1/N - i.e. tokens are routed to each expert with equal probability.
Expert choice
Instead of routing each token to the top k experts, Zhou et al (2022) solve the load balancing problem by letting each expert select the top t tokens from each sequence. This means that informative tokens can be processed by as many experts as necessary and uninformative tokens - e.g. padding tokens or stop words - can be ignored.
Dispensing with the requirement that the same amount of compute is used for every token appears to be a productive strategy: expert choice models train twice as fast as top-k experts models and perform better on GLUE and SuperGLUE language understanding benchmarks.
Komatsuzaki et al (2022) and Shen et al (2023) also observe that expert choice models outperform top-k experts models.
Soft mixtures of experts
Puigcerver et al (2023) propose a variant of expert choice routing, which they call a soft mixture of experts. In this model, experts act on sequences not tokens: each expert processes a weighted combination of all of the tokens in the input sequence. The weights are unique to each expert and are learned. Conceptually, the scientific expert places a greater emphasis on the scientific content in the sequence and the legal expert places a greater emphasis on the legal content.
As in expert choice models, each expert is utilised equally by design, so the load is never unbalanced: experts are never oversubscribed; nor do they sit idle. However, tokens are not processed equally: the emphasis an expert places on each token depends upon the learned weights. As each token is fractionally processed by each expert, these models are technically not sparse. However, as the emphasis on each token is uneven, they are not dense either.
One problem with this approach is that is solves load balancing by discouraging expert specialisation. Every sequence is processed by every expert, and so experts are trained to be generally useful. When experts are conditionally activated, a pressure to generalise arises from the load balancing loss term. However, in these models, equal utilisation is not a hard requirement; the importance assigned to load balancing can be tuned using the loss term hyperparameter α.
Training
Performance and training speed
Sparse mixtures of experts train faster than dense models. Fedus et al (2021) compare a dense Transformer (T5-Base) with various Switch Transformers, a mixture of experts model in which for the feedforward layers in each Transformer block tokens are either routed to their top expert or dropped. Trained using the same resources - 32 v3 TPUs - the mixtures of experts achieved the same performance the dense transformer in 1/7th of the time.
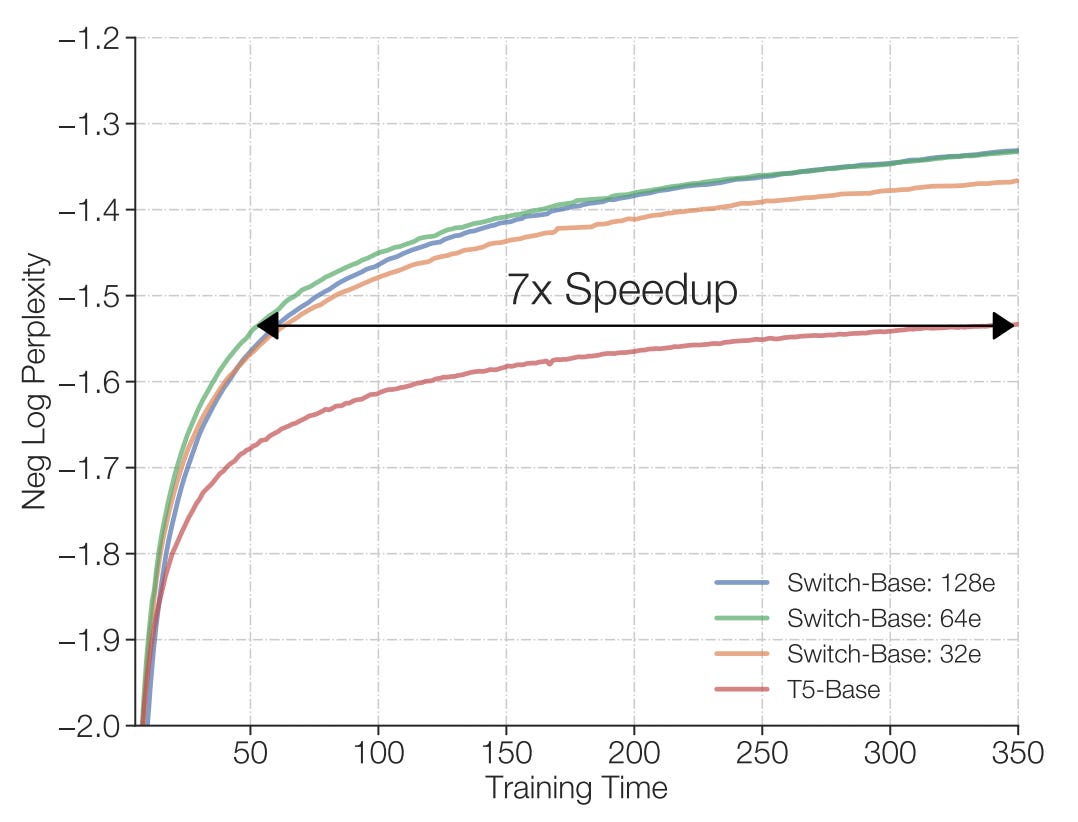
Moreover, compared to a larger dense model (T5-Large), a Switch Transformer with 64 experts trained 2.5 times faster, despite using only 2/7ths of the compute.

Changing the routing model unlocks further performance gains. Zhou et al (2022) observe that expert choice models train twice as fast compared to top-k expert routing models, including Switch Transformers.
Scaling
Sparse models are promising because they enable the number of parameters to be increased separately from the number of floating point operations required. Dense models have predictable scaling laws: provided they are not bottlenecked by an absence of high-quality training data, as the number of parameters is increased, the cross-entropy loss decreases as a power law.
Sparse models also demonstrate consistent performance increases when scaled:
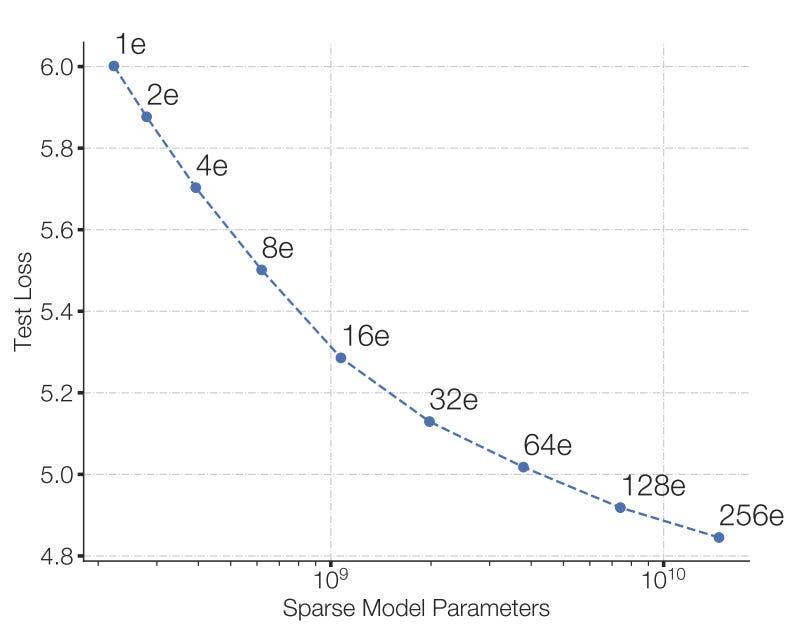
Clark et al (2022) observe that this relationship holds for other routing algorithms (the Sinkhorn algorithm, reinforcement learning and hashing the tokens). However, the scaling law they fit deviate from the power-law relationships observed in dense models. Instead, the authors find that the performance improvement obtained by adding more experts decreases as the models become larger. Once a dense model obtains ~900 billion parameters, the authors predict there will not be a further improvement to using a sparse mixture of experts. A strong caveat to this prediction must be made: the models used to fit the curve predate the Chinchilla paper, which counsels that parameters and training tokens should be scaled equally. Instead, each of the models were trained on 130 billion tokens.

In dense models, increasing the number of parameters makes a model more sample efficient - i.e. it trains faster. As Figure 2 shows, this also obtains for mixtures of experts: as the number of experts - and thus parameters - is increased, models require fewer samples to achieve the same level of performance.
Instabilities
Compared to dense transformers, sparse mixtures of experts are more prone to suffering from training instabilities. These occur when, instead of decreasing, the loss function diverges to infinity. Mixtures of experts are particularly afflicted because they contain more exponential functions, which compound the roundoff errors that arise from mixed precision training.
To reduce computation and communication costs, large neural networks store weights as float32 but operate on them as bfloat16. float32 uses 1 bit to represent the sign, 8 bits to represent the exponent and 23 bits to represent precision. bfloat16 has the same range as float32, but uses 1 bit to represent the sign, 8 bits to represent the exponent and only 7 bits to represent precision. Consequently, the roundoff errors for bfloat16 are several orders of magnitude higher. Figure 6 shows how these errors are worse for large, positive numbers; a similar pattern exists for negative numbers.

Mixtures of experts contain more exponential functions than dense models, because of the softmax function in their routers. Compared to the other operations in a neural network (e.g. addition or matrix multiplications), exponential functions are numerically unstable: a small change in the input - which might be caused by a roundoff error - can result in a large change in the output. This problem is particularly acute for high magnitude inputs, as the roundoff errors are larger.
Zoph et al (2022) demonstrate that penalising high magnitude inputs to the router’s softmax function improves training stability without reducing the model’s performance. Let T be the number of tokens in a batch and be N the number of experts. Let W be the router’s weights and X be the token representations in the batch. Then, letting β be a hyperparameter that reflects its importance, define the auxiliary Z-loss term as follows:
This loss function is minimised when WX - the inputs to the router’s softmax function - are small. Computation of the router probabilities depends only on the relative magnitude of the logits, so penalising high inputs does not necessarily change these. The router probabilities determine which experts process a token and how the expert outputs are scaled. Consequently, numerical instabilities due to roundoff errors have a compounding effect.
The authors report that training instability can be further reduced by
‘jittering’ the inputs to the router’s softmax by multiplying them by a number drawn uniformly at random from [0.99, 1.01]
replacing multiplicative activations such as GELU gated linear units (GEGLUs) with rectified linear units and removing multiplicative normalisations such as root mean square error normalisation
applying dropout throughout the model.
Unfortunately, these methods also degrade the model’s accuracy.
Fine-tuning and instruction tuning
Sparse models perform well when training on large, diverse datasets. However, during fine-tuning, they are susceptible to overfitting and consequently may perform worse than their dense counterparts.
Mitigating this problem requires setting noisier hyperparameters. Zoph et al (2022) demonstrate that, in contrast to dense models, sparse models perform better at fine-tuning when the learning rate is higher and the batch size is smaller. Dropping out entire experts does not help, but increasing the dropout probability within each expert has a moderate, positive effect.

Sparse mixtures of experts benefit more from instruction tuning than dense models. Shen et al (2023) establish that, in the absence of instruction tuning, mixtures of experts do worse than dense models when evaluated or further fine-tuned on downstream tasks. However, once both types of model are instruction-tuned, mixtures of experts outperform dense models.
Upcycling
A useful trick, pioneered by Komatsuzaki et al (2022), is to ‘upcycle’ an existing dense model by initialising a mixture of experts from the dense model checkpoint. In a Transformer, this is done by training the router from scratch, but initialising the experts from the weights of the feedforward layers they replace. Holding compute constant and continuing training, upcycled mixtures of experts train faster than their dense base models.

So, if there already exists a dense model checkpoint, upcycling it to a mixture experts might improve performance. And, if there does not, given that training a mixture of experts is more complicated, training a dense model and then upcycling it might be a useful hedging strategy.
Distillation
After training, a sparse mixture of experts model can be distilled into a smaller, dense model. If all experts are equally utilised, a sparse model and a dense model should require the same amount of GPU memory. (The sparse model will have greater throughput and hence require large batch sizes.) However, if they are not, then training a mixture of experts and then distilling it into a dense model is still worth doing, as some of the performance gain is retained. Fedus et al (2021), for example, compare a sparse mixture of experts model to a dense T5-Base model that is 100 times smaller. The mixture of experts naturally performs better. However, distilling the weights of the mixture of experts model into the dense model preserves 29% of the performance gain.
Deployment
Mixtures of experts typically contain outrageously high parameter counts. Consequently, though the computation requirements are low, the memory requirements are extremely high and the model must be distributed across multiple GPUs. To do this without incurring accuracy or latency penalties requires paying close attention to expert provisioning and device allocation.
Model capacity
Despite the load balancing objective that is present during training, at inference time, expert utilisation is extremely unbalanced. Huang et al (2023) examine the expert activation patterns for state-of-the-art mixture of expert set-ups and observe that for language modelling and machine translation, a small number of experts are always allocated a large share of tokens; others are completely inactive. Machine translation is particularly bad, because there is high temporal correlation: if one sequence makes use of a particular expert, the probability that the next sequence will use that expert is higher.

This is a problem, because it makes it difficult to predict the correct capacity for each expert at inference time. If expert utilisation is roughly equal, then provisioning experts is straightforward. Let N be the number of experts in a model, T be the number of tokens in each batch and C be the capacity factor, a hyperparameter. Then, the naïve implementation is to statically provision on a GPU a fixed capacity of CT/N tokens for each expert. To make efficient use of GPU parallelism, the expert feedforward networks on each device are stacked as tensors. If an expert is oversubscribed, the additional tokens are dropped or routed to an expert with spare capacity. If an expert is undersubscribed, padding tokens are allocated instead. This means that the token representations can also be stacked as tensors, improving efficiency. The dimensions of the expert tensor is num_experts_on_device × CT/N × expert_output_dimension and the dimensions of the token representations tensor is num_experts_on_device × CT/N × token_representation_dimension. The two tensors are then multiplied together to compute the expert outputs.
When expert allocation is unbalanced, the oversubscribed experts will drop (or reroute) tokens, hurting performance. The undersubscribed experts will waste compute processing padding tokens. If the imbalance is slight, token dropping can be reduced by increasing the capacity factor. However, for extreme imbalances, this is extremely wasteful.
If expert utilisation can be accurately predicted ahead of time, then individual capacity factors can be set for each model. Huang et al (2023) demonstrate how this can be done by examining historical load data. The optimal allocation of experts to GPUs is isomorphic to the multiway number partitioning problem, which is NP-hard. This can be approximated using a greedy algorithm: at each step, the expert with the highest historical workload is allocated to the GPU with the smallest load. Unfortunately, this approximation is less effective if sequences are temporally correlated, as in machine translation. To fix this, an expert’s predicted workload needs to be increased by adding the historical workload of each of its correlated experts multiplied by the strength of the correlation and a scaling factor.
Caching
A further optimisation that can be made is to offload the least used experts onto the CPU. This can be implemented using a least recently used cache - and this would account for temporal correlations.6 If there is a cache miss, there is a latency penalty, as the required expert must be copied to a GPU for inference. Huang et al (2023) find that for a machine translation model with 128 experts, reducing the cache size from 128 to 64 decreases memory usage by ~15% but increases latency by ~0.15 seconds (i.e. ~2.5 times).
Block sparsity
GPUs are designed to perform the same computation multiple times in parallel; hence, they are more efficient at dense matrix multiplications compared to sparser operations. To exploit this efficiency, deep learning libraries - including those that specialise in training mixtures of experts - make heavy use of batched matrix multiplications. These require the batched matrices to have the same shape - and some libraries even require that the shapes are statically specified at compile time. This is the reason why, at inference time, expert capacity must be accurately predicted and why the inputs to the experts must be padded or truncated.
Matrix multiplication consists of the repeated application of the dot product between the rows of the first matrix and the columns of the second. To multiply large matrices together, the GPU breaks the input and output matrices into tiles. The output tiles are computed by stepping through the inner dimension of the input matrices tile by tile, multiplying them together and accumulating the result.

Gale et al (2022) observe that the forward and backward passes in a mixture of experts feedforward layer can be expressed as block sparse matrix multiplications. (In a block sparse matrix, the nonzero elements are clustered into square submatrices.) This is useful, because block sparse matrix multiplications can also be tiled, enabling them to exploit GPU parallelism. As the empty blocks in the output matrix do not need to be computed, in principle block sparse matrix multiplication can achieve the same throughput as batched dense matrix multiplication.

When implemented as a block sparse matrix multiplication, a mixture of experts feedforward layer can flexibly and efficiently handle unbalanced token assignments without needing to drop tokens or waste compute processing padding tokens. Gale et al (2022) provide the CUDA kernels required to do this. Their implementation achieves 98.6% of the throughput obtained by cuBLAS for batched dense matrix multiplications, evaluated on mixture of experts feedforward layers.

Using block sparse matrix multiplications decreased the training time required by 1.38 times for the smallest model and 4.35 times for the largest.
How to train a fast and accurate mixture of experts model
This advice will help you get to the state of the art as of August 2023.
The optimal number of experts is between 64 and 128. Mixtures of experts, as with dense models, obey scaling laws: more parameters (i.e. more experts) result in better performance. However, there are diminishing returns: after ~128 experts the curve starts to taper.
Use expert choice routing instead of routing each token to its top k experts. Zhou et al (2022), Komatsuzaki et al (2022) and Shen et al (2023) all find that this increases performance. If using top-k experts per token, Fedus et al (2021) and Clark et al (2022) find that k=1 is sufficient; this will reduce training and inference costs.
Penalise high magnitude inputs into exponential functions - in particular, the softmax operation in the routers. Exponential functions are numerically unstable and the bfloat16 representation that is used in mixed precision training has large roundoff errors at high magnitudes. Zoph et al (2022) observe this reduces training instability, but does not harm performance.
Train each expert on curated data from different distributions. Li et al (2022) note that experts trained on data split by provenance performed much better than experts trained on random data splits.
If you have an existing dense model, ‘upcycling’ it into a mixture of experts might be more efficient than training a new model from scratch.
Instruction-tune the model, but be aware that the optimal hyperparameters for training are not the optimal hyperparameters for fine-tuning. Shen et al (2023) establish that, in the absence of instruction tuning, mixtures of experts do worse than dense models on downstream tasks. However, once both types of model are instruction-tuned, mixtures of experts outperform dense models.
Use the MegaBlocks CUDA kernels implemented by Gale et al (2022). This method of provisioning experts never drops tokens, eliminates wasteful computation and trains faster.
Further reading
Papers
Blog posts
Davis Blalock (2023), ‘2023-3-19 arXiv roundup: GPT-4, Data deduplication, MoE optimizations’
Finbarr Timbers (2023), ‘Papers I’ve read this week, Mixture of Experts edition’
Videos
Zoph et al (2022) discovered that putting a dense feedforward layers immediately before or after each sparse layer improves performance. This is not due to the extra parameters, as adding dense feedforward layers elsewhere is less effective.
In GPT-3, for instance, the attention heads account for ~1/3 of the parameters.
Non-gradient based methods of routing tokens to experts include reinforcement learning, linear programmes and hash functions.
Using more layers in the router does not increase performance. The reason for this is because the router is not trained in isolation from the rest of the model: if more compute is needed, the other layers can adapt. William Fedus, Barret Zoph and Yannic Kilcher have a good discussion about improving the routing function on Yannic’s YouTube channel.
In Fedus et al (2021), k = 1.
Huang et al (2023) adopt a different policy instead. First, experts that are not active in the present batch are evicted. This is to account for the temporal correlation of inputs. Next, experts are evicted using a last in, first out policy. This is to ensure the expert with the shortest reuse distance remains in the cache.


